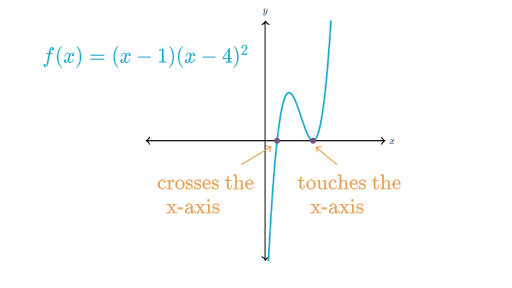Double Zero Math Graph
The graph has a turning point on the x-axis. X 6 twice.
3 4 Graphs Of Polynomial Functions Mathematics Libretexts
3 What is the Degree and name of this polynomial function.
Double zero math graph. Equivalently a regular graph has three distinct eigenvalues of which one is zero if and only if it is a multipartite graph. A double zero results from a function having a repeated root for example. When a function has a double zero then the graph does not cross over the x-axis at that point but rather it turns around.
X 7 twice. To directly determine if an equation is a function can be quite difficult at times. F x x2 2 x 3.
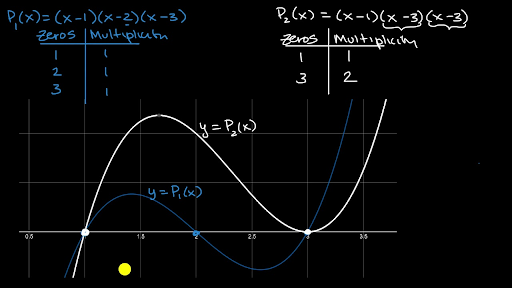
If the graph touches the x-axis and bounces off of the axis it is a zero with even multiplicity. Either a 0 or b 0. All four graphs have the same zeroes at x 6 and at x 7 but the multiplicity of the zero determines whether the graph crosses the x -axis at that zero or if it instead turns back the.
These are the 12 roots. What we need to do is show that for each x that we plug into the. This polynomial is of degree 3 4 5 12.
Look at the graphs of cubic polynomials below. Bifurcation theory is the mathematical study of changes in the qualitative or topological structure of a given family such as the integral curves of a family of vector fields and the solutions of a family of differential equationsMost commonly applied to the mathematical study of dynamical systems a bifurcation occurs when a small smooth change made to the parameter values the bifurcation. The graph touches the x-axis so the multiplicity of the zero must be even.
Because x 2 appears twice in the equation its corresponding zero 2 is called a double zero. X 7 once. This graph shows only two x-intercepts.
Now if we know that there is a double zero like in your case -1 that means not only is x - -1 a factor which if you simplify equals x 1. How does a double zero pass through the graph. Brendan explains what a double zero is - both graphically and algebraically.
For example notice that the graph of behaves differently around the zero than around the zero which is a double zero. A complete multipartite graph is. X 7 twice.
We see the zeros at -2 0 and 1. We already know that roots occur where the graph touchescuts the x axis so if a factor is of some squared form then the corresponding y values of the function would be positive. For example the second derivative of the position of an object with respect to time is the instantaneous acceleration of the object or the rate at which the.
0 is a root of odd multiplicity therefore 0 is a point of inflection. The sum of the multiplicities is the degree n. Zeros at x4 x3and x2 y-intercept at 024 63.
Find the roots of f x and sketch the graph of y f x. In calculus the second derivative or the second order derivative of a function f is the derivative of the derivative of fRoughly speaking the second derivative measures how the rate of change of a quantity is itself changing. Following is the graph of y x 6 x 2 2.
Here is the graph. Y x 6 2 x 7 x 6 twice. But actually since -1 is a double zero then x - -12 is a factor of the polynomial.
So x - -12 which equals x 12 is a factor. You can recognize the multiplicity of a zero from the polynomials graph as well. Study Math IB SL 32S.
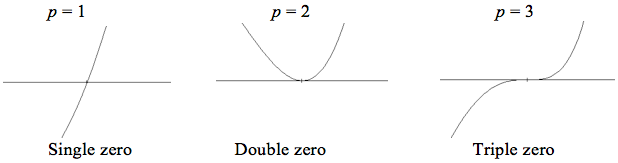
X2 2 x 3 x 1 x 3. The next zero occurs at latexx-1latex. The multiplicity of a zero is important because it tells us how the graph of the polynomial will behave around the zero.
Functions Unit Test flashcards from Jos ephs Freedom. The zero of 3 has multiplicity 2. 5 If the graph of a polynomial just touches the x-axis and then changes direction what can we conclude about the factored form of the polynomial.
If the graph crosses the x-axis at a zero it is a zero with odd multiplicity. Zeros at x3 x2 and x1 y-intercept at 012 Answer. Roots derived from factors of the form x-a2.
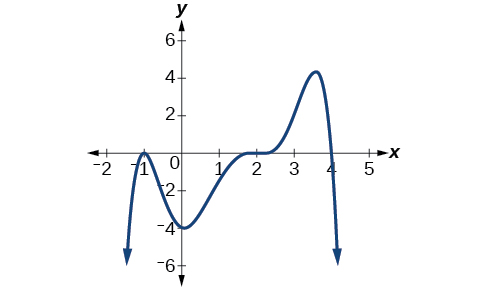
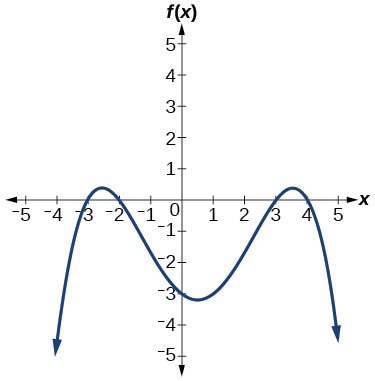
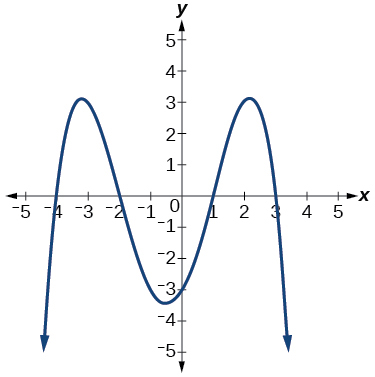
This graph has three x-intercepts so we know that the cubic function has three distinct Real zeros. This is a single zero of multiplicity 1. Y x 6 2 x 7 2.
If the graph crosses the x-axis and appears almost linear at the intercept it is a single zero. This polynomial is of even degree therefore the graph begins on the left above the x-axis2 is a root of even multiplicity therefore at 2 the graph is tangent to the x-axis. The only disconnected strongly regular graphs are finite sums of complete graphs of the same order 4.
0 0 0 2 2 2 2 3 3 3 3 3. Therefore the roots are 1 and 3. Starting from the left the first zero occurs at latexx-3latex.
See Lesson 37 of Algebra They are the x -intercepts of the graph. Specifically while the graphs crosses the -axis at it only touches the. So in conclusion a double zero or a double solution is where the graph crosses through the point TWICE on the x axis.
In fact every parabola of the form y. Double zero at x1 and triple zero at x3 Passes through the point 215 Answer. The graph looks almost linear at this point.
Class online or in Brainscape s iPhone. The x-intercept is where the graph of the function crosses the x-axis and the zero.
Multiplicity Of Zeros Of Polynomials Video Khan Academy

Polynomial Factors And Graphs Harder Example Video Khan Academy

What Does It Mean For A Quadratic Function To Have A Double Zero Quora
Zeroes Of Rational Functions Ck 12 Foundation

What Does It Mean For A Quadratic Function To Have A Double Zero Quora
Zeros And Multiplicity Polynomial Functions Article Khan Academy
Zeros And Multiplicity Polynomial Functions Article Khan Academy
Math Help Algebra Quadratics Theory Graphs
Quadratics Polynomials Of The Second Degree Topics In Precalculus
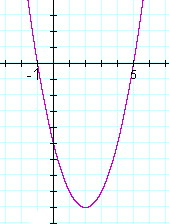
3 4e Exercises Mathematics Libretexts

Zeros And Multiplicity College Algebra

Zeros And Multiplicity College Algebra
3 4e Exercises Mathematics Libretexts

3 4 Graphs Of Polynomial Functions Mathematics Libretexts
Reading Graphs Of Polynomial Functions Part Ii Finite Math
Quadratics Polynomials Of The Second Degree Topics In Precalculus
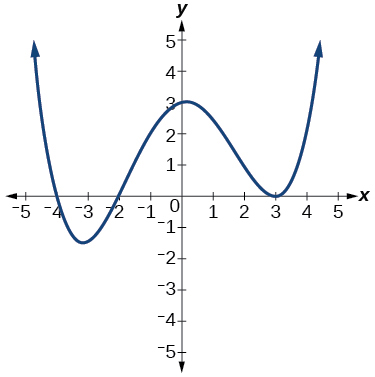
3 4e Exercises Mathematics Libretexts

Zeros And Multiplicity College Algebra
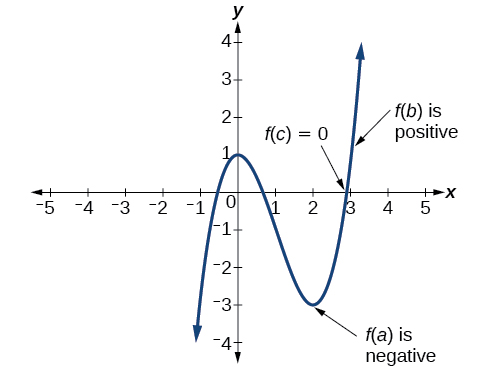
3 4 Graphs Of Polynomial Functions Mathematics Libretexts